Cyclone and Anticyclone. What is it, how do you remember it? Notations and definitions

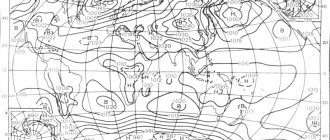
Difference between cyclone and anticyclone

A cyclone is an atmospheric vortex with:

low pressure in the center, and closer to the edges the pressure increases;
air movement towards the center;
rotation in the northern hemisphere counterclockwise, and in the southern hemisphere clockwise;
rainy weather.

An anticyclone is an atmospheric vortex with:

high pressure in the center, and closer to the edges the pressure decreases;
air movement away from the center;
rotation in the northern hemisphere clockwise, and in the southern hemisphere counterclockwise;
sunny weather.

(Here m is the mass of water passing through the conduit). But let's return to the vortex tube. Accelerating in its entrance scroll to high speed, the gas at the entrance to the cylindrical pipe 1 has a maximum tangential speed VR and the lowest thermodynamic temperature. Then it moves in pipe 1 along a cylindrical spiral to the far outlet, partially closed by cone 4. If this cone is removed, then the entire gas flow will freely exit through the far (hot) end of pipe 1. Moreover, the VT will be sucked through the hole in diaphragm 3 and part of the outside air. (The work of vortex ejectors, which have smaller dimensions than direct-flow ones, is based on this principle.) But by adjusting the gap between cone 4 and the edge of pipe 1, the pressure in the pipe is increased to such a value at which the suction of external air stops and part of the gas from pipe 1 begins exit through the hole in diaphragm 3. In this case, a central (paraxial) vortex flow appears in pipe 1, moving towards the main (peripheral) one, but rotating, as stated in [82], in the same direction. In the entire complex of processes occurring in the VT, there are two main ones, which, in the opinion of most researchers, determine the redistribution of energy between the peripheral and central vortex gas flows in it. The first of the main processes is the restructuring of the field of tangential velocities of rotating flows as they move along the pipe. The rapidly rotating peripheral flow gradually transfers its rotation to the central flow moving towards it. As a result, when the gas particles of the central flow approach diaphragm 3, the rotation of both flows is directed in the same direction, and occurs as if a solid cylinder, and not a gas, is rotating around its axis. Such a vortex is called “quasi-solid”. This name is determined by the fact that the particles of a rotating solid cylinder, in their movement around the cylinder axis, have the same tangential velocity dependence on the distance to the axis: Vr. =. ?r. The second main process in the VT is the equalization of the thermodynamic temperatures of the peripheral and central flows in each section of the VT, caused by turbulent energy exchange between the flows. Without this equalization, the internal flow, which has lower tangential velocities than the peripheral one, would have a higher thermodynamic temperature than the peripheral one. Since the tangential velocities of the peripheral flow are greater than those of the central flow, then after equalization of thermodynamic temperatures, the stagnation temperature of the peripheral flow moving to the outlet of pipe 1, half-covered by cone 4, turns out to be greater than that of the central flow moving to the hole in the diaphragm 3. Simultaneous action of the two of the described basic processes and leads, according to most researchers, to the transfer of energy from the central gas flow in the VT to the peripheral one and to the separation of gas into cold and hot flows. This idea of the work of VT remains recognized by the majority of specialists to this day. And the design of the VT has hardly changed since the time of Ranke, although the areas of application of the VT have been expanding ever since then. It was found that VTs that use a conical (small cone angle) pipe instead of a cylindrical one show slightly better operating efficiency. But they are more difficult to manufacture. Most often, VTs operating on gases are used to produce cold, but sometimes, for example, when working in vortex thermostats, both cold and hot flows are used [82]. Although the vortex tube has a much lower efficiency than other types of industrial refrigerators, which is due to the large energy costs of compressing the gas before feeding it into the VT, the extreme simplicity of the design and unpretentiousness of the VT make it indispensable for many applications. VT can operate with any gaseous working fluids (for example, water vapor) and at a wide variety of pressure differences (from fractions of an atmosphere to hundreds of atmospheres). The range of gas flow rates in VT is also very wide (from fractions of m3/hour to hundreds of thousands of m3/hour), and therefore the range of their capacities. At the same time, with an increase in the Diameter of the VT (that is, with an increase in its power), the efficiency of the VT also increases. When VT is used to produce cold and hot gas flows simultaneously, the pipe is made uncooled. Such VTs are called adiabatic. But when using only a cold flow, it is more profitable to use VTs, in which the pipe body or its far (hot) end is cooled by a water jacket or other method forcibly. Cooling allows you to increase the cooling capacity of the VT.

6.3. Vortex tube paradoxes

The vortex tube, which became that “Maxwell’s demon”, which separates fast gas molecules from slow ones, did not receive recognition for a long time after its invention by J. Ranke. In general, any processes and devices, if they do not receive a theoretical justification and scientific explanation, in our "enlightened" age are almost certainly doomed to rejection. This, if you like, is the flip side of enlightenment: everything that does not find an immediate explanation has no right to exist! And in Ranke's pipe, even after the appearance of the above explanation of her work, much remained and remains unclear. Unfortunately, the authors of books and textbooks rarely note the ambiguities of certain issues, but, on the contrary, more often seek to circumvent and veil them in order to create the appearance of the omnipotence of science. The book [82] is no exception in this regard. Thus, on its page 25, when explaining process of redistribution of energy in the VT by rearranging the velocity field of rotating gas flows and the emergence of a “quasi-solid” vortex, one can notice some confusion. For example), we read: “As the central flow moves towards... it experiences increasingly intense swirling from the external flow. In this process, when the outer layers twist the inner ones, as a result... the tangential velocities of the internal flow decrease, and the external ones increase.” The illogicality of this phrase makes one wonder if the authors of the book are trying to hide something that cannot be explained, to create the appearance of logic where there is none? Attempts to create a theory of VT by constructing and solving a system of gas-dynamic equations describing processes in VT have led many authors to insurmountable mathematical difficulties. Meanwhile, the study of the vortex effect by experimenters revealed more and more new features in it, the justification of which turned out to be impossible according to any of the accepted hypotheses. In the 70s, the development of cryogenic technology stimulated the search for new possibilities of the vortex effect, since other existing cooling methods - throttling, ejection and expansion of gases - did not provide a solution to the practical problems that arose in cooling in large volumes and liquefying gases with low condensation temperatures. Therefore, research into the operation of vortex coolers continued even more intensively. The most interesting results in this direction were achieved by Leningraders V. E. Finko. In his vortex cooler [83] with an VT having a cone angle of up to 14°, air cooling to 30°K was achieved. A significant increase in the cooling effect was noted with an increase in gas pressure at the inlet to 4 MPa and higher, which contradicted the generally accepted point of view that at a pressure of more than 1 MPa, the efficiency of HT practically does not increase with increasing pressure. This and other features discovered during tests of a vortex cooler with subsonic inlet flow velocities, which are not consistent with existing ideas about the vortex effect and the methodology adopted in the literature for calculating gas cooling with its help, prompted V. E. Finko to analyze these discrepancies in [84]. . He noticed that the stagnation temperatures of not only cold (Hox), but also “hot” (Hog) outgoing gas flows turned out to be significantly lower than the temperature T of the gas supplied to its VT. This meant that the energy balance in its VT did not correspond to the well-known Hilsch balance equation for adiabatic VT.

(6.5)

where I is the specific enthalpy of the working gas,

In the available literature, Finko did not find any works devoted to testing relation (6.5). In published works, as a rule, the fraction of cold flow JLI was determined by calculation using the formula

(6.6)

based on the results of temperature measurements Tovkh Gog Gokh. The last formula is obtained from (6.5) using the conditions: V.E. Finko creates the stand described in [84], on which, along with measuring the stagnation temperatures of flows, gas flow rates Ovx, Ox, Og were measured. As a result, it was firmly established that expression (6.5) is unacceptable for calculating the energy balance of VT, since the difference in the specific enthalpies of the incoming and outgoing flows in the experiments was 9-24% and increased with increasing inlet pressure or with decreasing temperature of the incoming gas. Finko notes that some discrepancy between relation (6.5) and test results was observed earlier in the works of other researchers, for example in [85, 86], where the discrepancy value was 10-12%, but was explained by the authors of these works by the inaccuracy of flow measurements. Further, V.E. Finko notes that none of the previously proposed mechanisms of heat exchange in HT, including the mechanism of countercurrent turbulent heat exchange, explains the high rates of heat removal from the gas, which lead to significant temperature differences recorded by him (~70°K and more) in its vortex cooler. He offers his explanation for the cooling of gas in the VT by “the work of vortex expansion of gas,” carried out inside the pipe over the portions of gas that previously entered there, as well as over the external atmosphere where the gas exits. Here we should note that in the general case, the energy balance of VT has the form [82]:

(6.7)

where Wokhl is the amount of heat removed per unit time from the VT body due to its natural or artificial cooling. When calculating adiabatic tubes, the last term in (6.7) is neglected due to its smallness, since the VTs are usually small in size and their heat exchange with the surrounding air through convection is insignificant compared to the heat exchange between gas flows inside the VT. And when artificially cooled VTs operate, the last term in (6.7) ensures an increase in the proportion of the cold gas flow leaving the VT. In the Finko vortex cooler there was no artificial cooling, and natural convection heat exchange with the surrounding atmospheric air was insignificant. Finko’s next experiment, described in [84], would seem to have no direct relation to issues of heat transfer in HT. But it is precisely this that makes us most strongly doubt not only the correctness of the previously existing ideas about the mechanism of heat exchange between gas flows in the VT, but also, in general, the correctness of the entire generally accepted picture of the operation of the VT. Finko inserts a thin rod along the axis of his VT, the other end of which is fixed in a bearing. When the VT is operating, the rod begins to rotate at a speed of up to 3000 rpm, driven by the rotating central gas flow in the VT. But only the direction of rotation of the rod turned out to be opposite to the direction of rotation of the main (peripheral) vortex gas flow in the VT! From this experiment we can conclude that the rotation of the central gas flow is directed opposite to the rotation of the peripheral (main) flow. But this contradicts the prevailing idea of “quasi-solid” rotation of gas in the VT. In addition to all this, V.E. Finko recorded infrared radiation of the band spectrum in the wavelength range of 5-12 microns at the exit of the cold gas flow from his VT, the intensity of which increased with increasing gas pressure at the entrance to the VT. Sometimes “blue radiation emanating from the core of the flow” was also visually observed. However, the researcher did not attach much importance to the radiation, noting the presence of radiation as an interesting accompanying effect, and did not even give the values of its intensities in [84]. This suggests that Finko did not connect the presence of this radiation with the mechanism of heat transfer in the VT. This is where we must again recall the mechanism proposed in Sections 4.4 and 4.5 for dumping “extra” mass-energy from a system of bodies being driven into rotation to generate the necessary negative binding energy of the system. We wrote that it is easiest for electrically charged bodies to release energy. When they rotate, they can simply emit energy in the form of electromagnetic waves or photons. In a flow of any gas there is always a certain number of ions, the movement of which in a circle or arc in a vortex flow should lead to the emission of electromagnetic waves. True, at technical frequencies of rotation of the vortex, the intensity of radio wave radiation by a moving ion, calculated using the well-known formula for cyclotron radiation at the fundamental frequency, turns out to be extremely low. But cyclotron radiation is not the only and far from the most important of the possible mechanisms for the emission of photons from a rotating gas. There are a number of other possible mechanisms, for example, through the excitation of gas molecules by ion-acoustic vibrations with subsequent illumination of the excited molecules. We are talking about cyclotron radiation here only because its mechanism is most understandable to the engineer who is reading this book. Let us repeat once again that when nature needs to radiate energy from a system of moving bodies, it has a thousand ways to do it. Moreover, from such a system as a gas vortex, in which there are so many possibilities for radiation that are understandable even with today’s development of science. V. E. Finko recorded a band spectrum of electromagnetic radiation with wavelengths =‹10 microns. The band spectrum is characteristic of thermal radiation of gas molecules. Solids produce a continuous spectrum of radiation [87]. From this we can conclude that in Finko’s experiments it was the radiation of the working gas, and not the metal casing of the VT, that was recorded. The thermal radiation of a rotating gas can consume not the rest mass of the emitting molecules or ions, but the thermal energy of the gas as the most mobile part of its internal energy. Thermal collisions between gas molecules not only excite the molecules, but also feed the ions with kinetic energy, which they emit in the form of electromagnetic energy. And it seems that the rotation of the gas somehow (perhaps through a torsion field) stimulates this radiation process. As a result of the emission of photons, the gas is cooled to lower temperatures than follows from the known theories of heat exchange between the central and peripheral vortex flows in the VT. Unfortunately, Finko's work [84] does not indicate the intensity of the observed radiation, and therefore nothing can yet be said about the magnitude of the power carried away by it. But he noted heating of the inner surface of the walls of the VT by at least 5°K, which could be due to heating by this particular radiation. In this regard, the following hypothesis arises about the process of heat removal from the central flow to the peripheral vortex gas flow in the VT. The gas of both the central and peripheral flows emits photons during their rotation. It would seem that the peripheral one should radiate more intensely, since it has a higher tangential speed. But the central flow is in an intense axial torsion field, which stimulates the emission of photons by excited molecules and ions. (This, in Finko’s experiments, proves the presence of a blue glow precisely from the “core” of the flow.) In this case, the gas of the flow is cooled due to the radiation leaving it, which carries away energy, and the radiation is absorbed by the walls of the pipe, which are heated by this radiation. But the peripheral gas flow, in contact with the pipe walls, removes this heat and heats up. As a result, the central vortex flow turns out to be cold, and the peripheral one is heated. Thus, the VT body plays the role of an intermediate body, ensuring heat transfer from the central vortex flow to the peripheral one. It is clear that when the VT body is made cooled, the heat transfer from it to the peripheral gas flow is reduced due to a decrease in the temperature difference between the pipe body and the gas in it, and the cooling capacity of the VT increases. This hypothesis also explains the violation of the thermal balance discovered by Finko, which we discussed above. Indeed, if part of the radiation leaves the VT through its outlets (and this part can be ~10%, judging by the geometry of the device used by Finko), then the energy carried away by this part of the radiation is no longer registered by instruments that measure the stagnation temperature of the gas at the pipe outlets. The fraction of radiation leaving the pipe especially increases if the radiation is generated predominantly near the opening of the diaphragm 3 of the pipe (see Fig. 6.5), where the gas rotation speeds are maximum. A few more words must be said about heating the peripheral gas flow in the VT. When V.E. Finko installed a gas flow “straightener” (lattice “brake”) at the “hot” end of his VT; the “hot” part of the outgoing gas flow after the “straightener” already had a temperature 30-60°K higher than Tovkh. At the same time, the share of the cold flow increased due to a decrease in the flow area for removing the “hot” part of the flow, and the temperature of the cold part of the flow was no longer as low as when working without a “straightener”. After installing the “straightener,” Finko notes a very intense noise when its VT operates. And he explains the heating of the gas when a “straightener” is placed in the pipe (which, as his estimates showed, could not heat up so much only due to the friction of the gas flow against the “straightener”) by the occurrence of sound vibrations in the gas, the resonator of which is the pipe. Finko called this process “a mechanism of wave expansion and compression of gas,” leading to its heating. It is clear that the inhibition of rotation of the gas flow should have led to the conversion of part of the kinetic energy of the flow into heat. But the mechanism of this transformation was revealed only in Finko’s work. The foregoing shows that the vortex tube still conceals many mysteries and that the ideas about its operation that have existed for decades require a radical revision.

6.4. Counterflow hypothesis in vortices

Vortex motion contains so much unexplored that there will be enough work for more than one generation of theorists and experimenters. And at the same time, vortex motion is apparently the most common type of motion in nature. Indeed, all those bodies (planets, stars, electrons in an atom, etc.), about which we wrote in section 4.1 that they perform circular motion, usually also move translationally. And when adding their rotational and translational movements, the result is a spiral movement. There are two main types of spirals: cylindrical helical spirals, which we discussed in section 4.3, and the Archimedes spiral, the radius of which increases with the number of turns. This is the appearance of spiral galaxies - the largest vortices in nature. And the superposition of rotational motion along the Archimedes spiral and translational motion along its axis also gives a third type of spiral - conical. Water moves along such a spiral, flowing out of the bath into the pipe at its bottom, and air in the tornado. Gas moves along the same conical spiral in technical cyclones. There, with each revolution, the radius of the particle trajectory decreases.

Rice. 6.6. Velocity profile of free submerged jets of varying degrees of twist [88]: a - direct-flow jet; b - weakly swirling jet; c — moderately swirling jet; d - strongly swirling closed jet; d - strongly swirled open jet; a - wall; b - hole in the wall; с- jet boundaries; d is the velocity profile at various distances from the wall; e is the jet axis; [Y is the axial speed.

But in a Finko vortex cooler, which has a conical vortex tube, the peripheral gas flow moves along an expanding conical spiral, and the counter axial flow moves along a tapering one. This configuration of flows in the VT and technical cyclone is determined by the geometry of the walls of the apparatus. When considering a vortex tube in Section 6.2, we wrote that reverse axial flow in it occurs when the gas outlet through the far (hot) end of the tube is partially blocked, and excess pressure is created in it, forcing the gas to seek a second outlet from the tube. This explanation of the occurrence of counter axial flow in the VT is currently generally accepted [82]. But experts in swirling jets, which are widely used, for example, to create torches in the burners of thermal power plants, note that a counterflow along the axis of the swirling jet also occurs in the absence of walls of the apparatus. A study of the velocity profiles of free submerged jets (see Fig. 6.6) shows that the reverse axial flow increases with increasing degree of jet twist [88]. The physical cause of the counterflow has not been clarified. Most experts believe that it appears because with an increase in the degree of twist of the jet, centrifugal forces throw particles of its gas to the periphery, as a result of which a rarefaction zone is created at the axis of the jet, into which atmospheric air, located in front along the axis of the jet, rushes. But in works [89, 90] it is shown that the reverse flow is associated not so much with the static pressure gradient in the jet, but with the ratio of the tangential and axial (axial) components of its velocity. For example, jets formed by a swirler with a tangential blade apparatus, with a blade angle of 40-45°, have a large vacuum in the axial region, but do not have reverse flows. Why they are not there remains a mystery to specialists. Let's try to unravel it, or rather, explain in a different way the reason for the appearance of axial countercurrents in swirling jets. As we have repeatedly noted, the easiest way to remove “extra” mass-energy from a system set into rotation is by emitting photons. But this is not the only possible channel. We can also propose the following hypothesis, which at first will seem incredible to some mechanics. The path to this hypothesis was long and was made by more than one generation of physicists. Viktor Schauberger, a brilliant Austrian genius, a forester who studied physics in his spare time, who devoted a lot of time in the 20s to understanding vortex motion, noticed that with the spontaneous spinning of water flowing into a pipe from a bathtub, the time for emptying the bathtub decreases. This means that in the vortex not only the tangential, but also the axial flow velocity increases. By the way, this effect has long been noticed by beer lovers. At their competitions, in an effort to get the contents of the bottle into their mouths as quickly as possible, they usually first swirl the beer in the bottle very hard before tilting it back. We don’t know whether Schauberger loved beer (what Austrian doesn’t love it!), but he tried to explain this paradoxical fact by the fact that in a vortex the energy of thermal motion of the molecules in it is converted into the kinetic energy of the axial movement of the jet. He pointed out that although such an opinion contradicts the second law of thermodynamics, no other explanation can be found, and the decrease in the temperature of water in a whirlpool is an experimental fact. Based on the laws of conservation of energy and momentum, it is usually believed that when a jet twists into a longitudinal vortex, part of the kinetic energy of the translational motion of the jet is converted into the energy of its rotation, and they think that as a result the axial speed of the jet should decrease. This, as stated, for example, in [88], should lead to a decrease in the range of free submerged jets when they swirl. Moreover, in hydraulic engineering they usually do their best to combat fluid turbulence in devices for its overflow and strive to ensure irrotational laminar flow. This is explained by the fact, as described, for example, in [91], that the appearance of a vortex cord in a liquid flow entails the formation of a funnel on the surface of the liquid above the entrance to the drain pipe. The funnel begins to vigorously suck in air, the entry of which into the pipe is undesirable. In addition, it is mistakenly believed that the appearance of a funnel with air, which reduces the proportion of the inlet hole cross-section occupied by liquid, also reduces the flow rate of liquid through this hole. The experience of beer lovers shows that those who think so are mistaken: despite the decrease in the proportion of the hole’s cross-section occupied by the liquid flow, the latter, when the flow rotates, flows out through the hole faster than without rotation. If L. Gerbrand, whom we wrote about in section 3.4, sought to achieve an increase in the power of hydroelectric power plants only by straightening the flow of water to the turbine and gradually narrowing the conduit so that the water acquired the highest possible forward speed, then Schauberger equipped the tapering conduit with screws guides that twist the water flow into a longitudinal vortex, and at the end of the conduit he places an axial turbine of a fundamentally new design. (Austrian Patent No. 117749 dated May 10, 1930) The peculiarity of this turbine (see Fig. 6.7) is that it does not have blades, which in conventional turbines cross the flow of water and, breaking it, waste a lot of energy on overcoming the forces of surface tension and adhesion of water molecules. This leads not only to energy losses, but also to the appearance of cavitation phenomena, causing erosion of the turbine metal. The Schauberger turbine has a conical shape with spiraling blades in the form of a corkscrew, screwing into a swirling flow of water. It does not break the flow and does not create cavitation. It is not known whether such a turbine has ever been implemented in practice, but its design certainly contains very promising ideas. However, we are interested here not so much in Schauberger’s turbine as in his statement that the energy of thermal motion of water molecules in a vortex flow can be transformed into the kinetic energy of a water flow. In this regard, the most interesting are the results of experiments carried out in 1952 by W. Schauberger together with Professor Franz Popel at the Technical College of Stuttgart, which are described in [92] by Joseph Hasslberger from Rome. Studying the influence of the shape of the conduit channel and the material of its walls on the hydrodynamic resistance to the swirling flow of water in it, experimenters discovered that the best results are achieved with copper walls. But the most surprising thing is that with a channel configuration resembling an antelope horn, friction in the channel decreases with increasing water speed, and after exceeding a certain critical speed, water flows with negative resistance, that is, it is sucked into the channel and accelerates in it [92].

Rice. 6.7. Schauberg turbine

Hasslberger agrees with Schauberger that here the vortex transforms the heat of the water into the kinetic energy of its flow. But oh. However, Hasslberger points out, modern thermodynamics is not able to explain many other natural phenomena [93]. And this is where the theory of motion can help to understand why vortex motion ensures, seemingly contrary to the prevailing ideas of thermodynamics, the conversion of the heat of a swirling flow of matter into the energy of its axial motion in accordance with formula (6.4). The twisting of the flow in a vortex forces part of the heat, which is part of the internal energy of the system, to be converted into kinetic energy of the translational motion of the flow along the axis of the vortex. Why along the axis? Yes, because then the velocity vector of the acquired translational motion turns out to be perpendicular to the vector of the instantaneous tangential velocity of the rotational motion of particles in the flow and does not change the value of the latter. In this case, the law of conservation of angular momentum of the flow is observed. In addition, the acceleration of particles in the direction perpendicular to the direction of their main (circular) motion in the vortex leads to a relativistic increase in their transverse, rather than longitudinal, mass. Much was written about the need to separately take into account the transverse and longitudinal masses of elementary particles* (This is reminiscent of the separate calculation of the longitudinal and transverse Doppler effect.) in the initial stage of the development of SRT (see, for example, [94].) Namely, the longitudinal mass (corresponding in this case tangential velocity of particles in the vortex) determines the magnitude of centrifugal forces during circular motion. When part of the internal energy of the system is converted into kinetic energy of the axial (axial) motion of bodies in it, centrifugal forces do not increase. Therefore, the energy of the emerging axial motion appears to have disappeared from the problem of circular motion, which is mathematically equivalent to its departure from the rotating system without any emission of photons. But the law of conservation of momentum of the system requires that if a vortex flow acquires an axial momentum, some other body (for example, the body of a vortex apparatus) simultaneously acquires an impulse of the same absolute value in the opposite direction. In closed vortex devices, for example in vortex tubes, and also when there is no contact of the vortex flow with the walls of the device (as in some cases of free swirling jets), the axial part of the flow, which has a lower tangential speed than the peripheral part, is forced to acquire the reverse impulse. However, the recoil impulse can also be carried away by an axial (axial) flow of photons or neutrinos generated during rotational motion, which will be discussed in the eleventh chapter. This is, in general terms, the true, from our point of view, reason for the appearance of countercurrent both in vortex tubes and in swirling jets.

Conclusions to the chapter

1 Atmospheric vortices are characterized by predominantly right-handed air movement in them and the presence of an “eye of the storm” - a central zone of slow movements or calm. 2. Tornadoes still have a number of mysteries: ultra-high speeds of air and objects trapped in them, extraordinary lifting force exceeding the pressure force of the air flow, the presence of glows, etc. 3. The thermal energy of masses of moist air is converted into energy of movement in atmospheric vortices. In this case, energy concentration occurs, which at first glance contradicts the principles of thermodynamics. 4. The contradiction with thermodynamics is removed if we assume that atmospheric vortices, in accordance with the requirements of the theory of motion, generate thermal (infrared and microwave) radiation. 5. The discovery in the 30s by J. Ranquet of the effect of gas separation in a vortex tube into hot near-wall and cold axial vortex flows marked the beginning of a number of new directions in technology, but still does not have a sufficiently complete and consistent theoretical explanation. 6. Works of V.E. Finko in the 80s cast doubt on the correctness of some generally accepted ideas about the processes in a vortex tube: the energy balance in it, the mechanism of countercurrent turbulent heat exchange, etc. 7. V.E. Finko discovered that the cold axial counterflow in the vortex tube has a direction of rotation opposite to the direction of rotation of the main (peripheral) gas flow, and that the gas vortex tube generates infrared radiation of the band spectrum, and sometimes also blue radiation emanating from the axial zone. 8. Placing a brake at the hot end of the vortex tube—a gas flow straightener—results, as V.E. discovered. Finko, to the emergence of intense sound vibrations in the gas, the resonator of which is the pipe, and to their strong heating of the gas flow. 9. A mechanism is proposed for heat removal from the axial counterflow of gas in the vortex tube to the peripheral flow due to radiation stimulated by the acceleration of gas rotation by the axial flow of photons, which heat the walls of the vortex tube, and heat is transferred from them to the peripheral gas flow washing them. 10. Axial counterflow occurs not only in vortex tubes, but also in free swirling jets, where there are no walls of the apparatus, the reason for which has not yet been fully elucidated. 11. W. Schauberger pointed out in the 30s that in a vortex, part of the energy of the thermal movement of the molecules in it is transformed into the kinetic energy of the axial movement of a water jet, and proposed using this. 12. The theory of motion explains the Schauberger effect by the fact that the swirling of the water flow causes part of the thermal energy of the molecules, which is the internal energy of the flow, not to leave the swirling flow in the form of radiation, but to be transformed into the kinetic energy of the flow in the direction perpendicular to the tangential speed of twisting, along axis of the vortex flow. The latter is required by the law of conservation of angular momentum of flow. And the law of conservation of momentum along its axis of rotation requires that in this case either a countercurrent appears, or axial radiation of photons or neutrinos is generated, compensating for the change in the longitudinal momentum of the flow.

Content

Further

Our site is a library premises. Based on the Federal Law of the Russian Federation “On Copyright and Related Rights” (as amended by Federal Laws dated July 19, 1995 N 110-FZ, dated July 20, 2004 N 72-FZ), copying, saving on a hard drive or other method of saving works located on This library is strictly prohibited . All materials are presented for informational purposes only.

What is the difference between a cyclone, hurricane, typhoon, cordonaso and willy-willy?

Tropical cyclones are also divided by geographic location:

North and South America - hurricane;
Far East and Southeast Asia - typhoon;
The Pacific Ocean off the western coast of Central America and Mexico - Cordonazos;
The Timor Sea off the northwestern coast of Australia is a willy-willy.

Each severe tropical cyclone is given a name (Idai, Irma, Fani), this is done in order to avoid confusion in the press or in other ways of mentioning it.

Mesocyclone

It's an air vortex

, with a diameter of 2 to 10 km, which is formed during a convective storm, that is, the air rises up and rotates around a vertical axis. This is usually associated with a localized area of low pressure during a thunderstorm, which can produce strong surface winds and hail.

If the right conditions exist, progression into
supercells
, which are nothing more than huge rotating storms from which a tornado can form. This incredible phenomenon occurs in conditions of high instability and strong winds at high altitudes. To see them, it is advisable to travel to the Great Plains of the United States and the Pampean Plains in Argentina.

And we'll leave it at that. What do you think about this special?

What is the difference between a cyclone, tornado and tornado?

In principle, a tornado and a tornado are synonyms. However, sometimes they are distinguished by calling vortices swirling over water a tornado, and vortices over land a tornado.

Tornado in Cala Ratjada, Mallorca, Spain, September 11, 2005

A tornado (tornado) is a very strong whirlwind that forms under thunderclouds in hot weather. It can extend from the ground or water like a huge dark gray rotating funnel or pillar. This phenomenon is mainly characteristic of the territories of Asia, North America and Europe.

What does the word "tornado" mean?

Photo of a tornado
Most of the phenomenon occurs in North American territories. This is where disasters take their name. In Spanish, "tornado" means "spinning". Wind whirlwinds began to be called tornadoes by Spanish colonists who arrived to conquer new territories.

In the territories of Russia, the phenomenon was called a familiar tornado.
The word comes from the Old Russian "smarch" or "smirch", which means cloud. Thus, the concepts “tornado” and “tornado” are synonymous. They describe the same phenomenon. Interesting fact : once a case was recorded when a heavy train weighing 80 tons was carried away by a whirlwind. The whirlwind dragged him 40 meters from the tracks.

How does a cyclone form?

A cyclone occurs in places of low atmospheric pressure. When a warm air mass collides with a cold one, it is called an atmospheric front. An uneven front boundary forms in some place and some of the warm air is pushed back by dense cold air.

This part of the warm air turns back and opposes the general movement of the warm air mass. Then, due to an increase in atmospheric pressure, this part of the warm air must somehow go to the side and swirl.

The so-called ellipsoidal rotation of air occurs (ellipsoidal rotation is when the ellipse rotates around its minor axis) with denser “walls” along the periphery, and the temperature inside rises.

This vortex covers the entire part of the warm air mass located near the front. Then, little by little, she is completely drawn into the torsion.

Tropical Cyclone Debbie, March 27, 2021, Queensland, Australia

Classification of tornadoes

Scientists identify several types of atmospheric vortices.

Types of tornadoes

In the form of a whip or scourge, which are mainly observed above the sea surface. They are smooth on the outside, narrow and sinuous. Meeting such vortices is fraught with serious problems.

Scourge-like tornado
Vague vortices that look like clouds above the ground. They constantly spin and can destroy large areas. They are extremely dangerous due to the fact that in such a cloud there is not one funnel, but several at once. They can cover huge areas.

Blurry tornado
Composite tornadoes from several whips at the same time. They revolve around a large central funnel and are extremely dangerous, just like the previous type. They destroy not one, but several territories at once.

Composite tornado
Tornadoes appearing from behind volcanoes in the form of a column of fire. They spread fire to nearby areas and create fires.

Fire tornadoes
Waterspouts are dangerous because there is nowhere to hide in the sea. The crew of the ships can only hope for a favorable outcome.

Waterspouts
Ground tornadoes are very rare. They are caused by serious natural disasters such as earthquakes. They are thin, rope-like. In the center of the pillar, lumps of soil writhe, and below there is a thick mass of mud.

Earth tornado
Snow tornadoes appear due to snowstorms and strong blizzards.

Snow tornado
Sandspouts are a separate species found in desert areas.

Sandspout

A sand tornado occurs in an unusual way. It is formed not in the clouds, but near the ground. The sand becomes very hot under the sun, and then air currents begin to gather in this area. The sand begins to gradually rotate, a large voluminous funnel is formed, which can exist and move for a long time.

What's the weather like in Anticyclone?

In an anticyclone, the air does not rise, but falls, and, as a rule, it is quite dry. Therefore, the weather during this period is always clear, dry, and partly cloudy. The temperature in summer is high, the weather is hot; winter is frosty. Atmospheric fronts, unlike cyclones, never occur at the center of anticyclones.

Interesting materials:

How to get a photo from a contact? How to get contacts from the cloud? How to export contacts from Android to Google? How to export contacts from Android to iPhone? How to export contacts from Android? How to export contacts from Gmail? How to export contacts from Google? How to export contacts from Google? How to export contacts from iPhone? How to export contacts from Gmail?